図１は、屈折率niの入射媒質から屈折率ntの透過媒質に光ビームが進行する様子を示す。
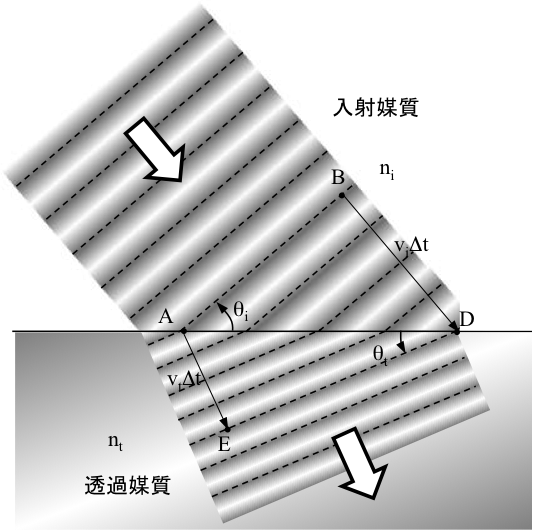図１ 波動の屈折通過。媒質表面の原子が２次波を放射して、それらが強め合うように重なって屈折ビームを構成する。
ここでは、ni < nt とする。速度viで進む波面上にある点Bが、時間 Δt後に点Dに到達したとする。同じ波面上にある点Aは速度vtで、同じ時間で点Eに達する。vi > vtであるからAE (=vtΔt)< BD(=viΔt)となり、波面は折れ曲がる。入射波面・透過波面が境界面となす角度をθi・θtとする。直角三角形ABD・AEDは、斜辺ADを共有するから、
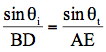
BD = viΔt・AE = vtΔtであるから、
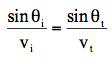
両辺に真空中の光速度cを掛けて、ni = c/vi・nt = c/vtを考慮すると、
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。