反射の法則

光学的に高密度な媒質の平面へ、真空から平面波がある角度で入射する場合を考える(図１)。

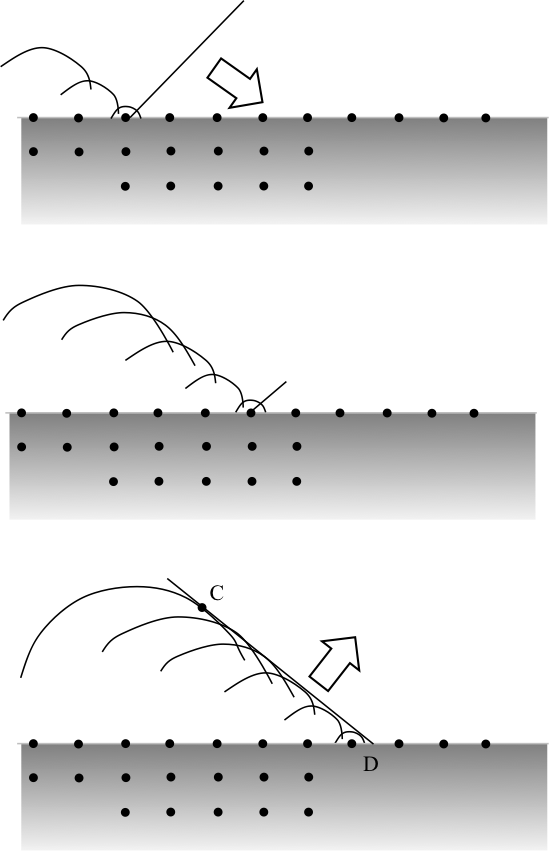
図１　散乱の結果としての波動の反射。

入射波の波面が媒質に侵入するに従って、媒質分子のエネルギーを順次高めていく。各分子は、半球状の波とみなせる光子流を入射媒質側に放射する。波長は分子間距離と比較して十分大きいので、強め合う干渉をおこなう特定方向のみに散乱光は向かい、単一の反射ビームとなる。これと異なり、波長が短いX線の場合、あるいは、散乱体の間隔が波長より大きい回折格子の場合は複数本の反射ビームが生じる。反射方向は、反射散乱体間で与えられる位相差で決まる。この位相差は、(原子間隔と)入射角で決定される。図２で、線分AB・CDは入射波・反射波の波面を示す。

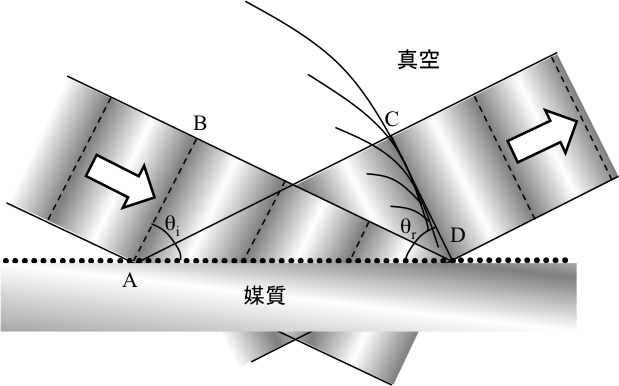
図２　散乱の結果としての波動の反射

平面波が左から入射して右に反射している。反射波面CDは、AからDにある表面原子よる散乱波で構成されている。
Aからの波がCに到達したとき、原子Dが放射して波面CDが完成する。