下記に加え、フレネルの公式もご覧下さい。
振幅および放射束密度の反射率・透過率を考察する。また、反射・屈折に伴う位相変化を考える。
振幅係数
垂直入射に近い(θi≈0)ときtanθi≈ sin θiだから、振幅反射係数r//・r⊥と振幅透過係数t//・t⊥は、フレネルの公式の式２１から、
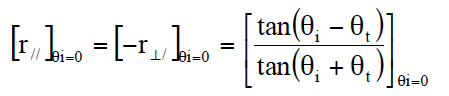
正弦関数を展開しスネルの法則を用いると、
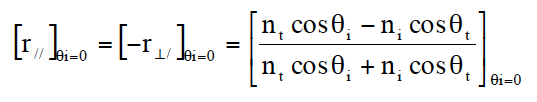
(式１)
無料ユーザー登録
続きを読むにはユーザー登録が必要です。登録することで3000以上ある記事全てを無料でご覧頂けます。
SNS（Facebook, Google+）アカウントが持っているお客様は、右のサイドバーですぐにログインできます。 あるいは、既に登録されている方はユーザー名とパスワードを入力してログインしてください。
*メールアドレスの間違いが増えています。正しいメールアドレスでないとご登録が完了しないのでお気を付けください。