どんな波形でも、適当に選んだ正弦波を重ね合わすことで合成できる。波長がλ1とλ2の調和波をからなる合成波は非調和波である。
一方の波形のN1サイクルと他方の波形N2サイクルの間に λ1N1= λ2N2なる関係があれば、両者は同一の位相関係に復帰し、
合成波は周期的となる。各成分波の初期位相は同一である必要はない。各成分波の振幅を周波数に対応して示すと周波数スペクトルとなる。
周期関数を解析する美しい数学的手法としてフーリエの定理がある。定理は、「空間周期λをもつ関数 f(x) は、λの整数分の1 の波長をもつ
調和関数の和によって合成できる」と述べる。数学的に表現すると、
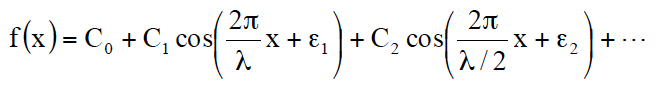
(式1)
となる。ここで、C は任意定数である。
三角関数の等式
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
