反射・屈折を含む光の伝搬は、フェルマーの原理を用いて考察することができる。 ユークリッドは、“任意点Sから任意点Pへ反射面を経由して進む光は、とりうる経路の中で最短の経路をたどる”と主張した(図1)。
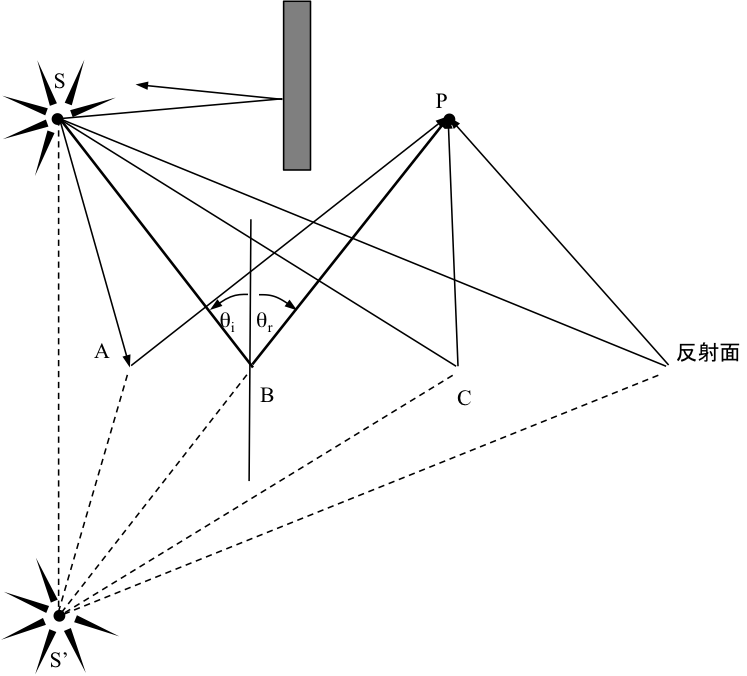
図1 光源SからPにある観測者の目に至る最短経路
図には複数の取りうる経路を描いてある。Sの像S’から光線が出ているものとしても、Pに至る距離は変わらない。複数の経路の中で、θi=θrとなる真っ直ぐな経路
S’BPが最短となるのは明らかである。この議論を発展させて、1657年にフェルマーは最小時間原理を提唱した。境界を挟む点Sから点Pに至る光線は明らかに最短距離ではない(図2)。
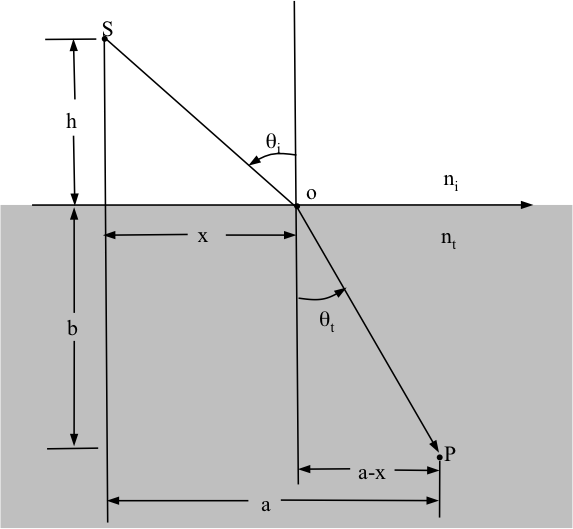
図2 フェルマーの原理の屈折への応用
これに対して、“光がたどる経路は、最小時間で通過できる経路である”と最小時間原理は述べる。最小時間原理を応用して屈折を考察する(図2)。xを変化させて、点Sから点Pまで移動する時間tを最小にすることを考える。移動時間tをxの関数として求めると、
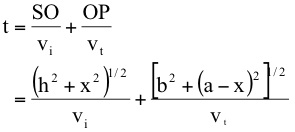
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
