内部全反射が生じているときの電界を考察する。振幅反射係数r⊥・r//は、フレネルの公式を書き換えて、
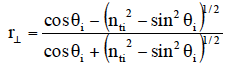
(式1)
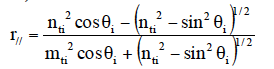
(式2)
となる。sin θc= ntiであるから、θi> θcではsin θi> ntiとなり、r⊥もr//も複素数になる。
この場合も、r⊥r⊥* = r//r//*=1(*は複素共役を示す)つまりR = 1 であり、Ir= IiでIt= 0を意味する。
透過波は、平均すれば境界を越えてエネルギーを運ぶことはない。このときの電界の様子を考察する。透過波の電界は、
![]()
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
