導体を強制減衰振動子の集合とみなす。その一部は自由電子に対応し復元力を持 たない。他は原子に束縛されている(分散を参照)。
金属の光学的性質は主に、 伝導電子が決めている。振動している電子の変位 x(t) は、
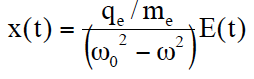
(式1)
で与えられる。復元力がないときは ω0 = 0 であり、(誘電体のときとは異なり、) 変位は電界に対して180°位相ずれがある(図)。
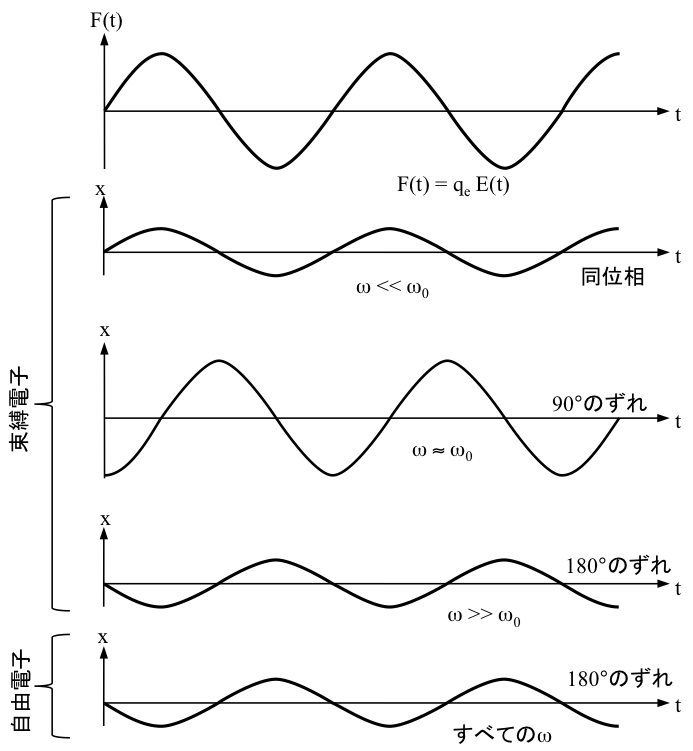
図 束縛電子および自由電子の振動
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
