中空間周波数誤差:性能不足の隠れた犯人
中空間周波数(MSF)エラーは、ゼルニケ多項式スペックよりも周波数的に高く、表面粗さよりも低い。MSFエラーは、ハイパフォーマンス光学システムに悪影響を与えることになりうるので、適切に計測する高精度測定が必要である。
ハイパフォーマンス光学システムというと、MSF エラーが幅広い範囲でアプリケーションに影響する。例えば、映画撮影用光学機器では、MSF エラーは、「ボケ味」の品質に甚だしく影響する、特にMSF が非球面に存在する場合だ(ボケ味は焦点外におけるブラーの美的品質)。高解像度監視システムでは、MSFエラーは画像コントラスト全体を悪化させる。
しかし、現在導入されている多くのハイパフォーマンスシステムでは、MSFエラーは軽視されているか、見過ごされているかのいずれかだ。MSFの懸念が明らかになった時でさえ、ほとんどの設計者のモデリング作業は、製造工程についての特殊知識なしには極めて困難である。例えば、光学技術者は、研磨工程における特徴的なMSF である「フィンガープリント」についてよく知っているが、設計者が公差に取り入れるような仕方で、そのデータを分離することは極めて稀である。
MSF エラーの影響と原因を理解するために、先ず表面を周波数成分で記述する必要がある。そのために、フーリエ解析を用いて周波数成分で表面を「分類」する。次に、その結果は、パワースペクトル密度( PSD )プロットとしてプロットされる。単位l 2l(l =長さ)で表す特殊周波数「ビン」は、単位l -1で表す空間周波数に対してプロットされる。
プロットの低い周波数端では、一般にエラーが、形状、パワー、不規則性もしくはゼルニケ多項式スペックで説明される。高い周波数端では、エラーは一般に表面粗さスペック、Ra(絶対値の算術平均)やRq(二乗平方根値)で説明される。周波数間のエラーは、MSF、リップル、うねり、平滑度、スロープエラーなど、呼び方が多様である。加えて定義付けが異なり、劇場の聴衆や戦闘シーンを批評するアナリストは最も強い映像コントラスト、深み、奥行きを得ようとするが、設計者やメーカーは、光学システムのパフォーマンスを理解しコントロールするために、全体的なスペクトラムエラーに考慮を払わなくてはならない。
図1は、ダイヤモンド旋盤で研磨した表面を3D光プロファイラ(ザイゴ社のNewView)計測のPSDプロットを示している。1.8nmと1.3nmで、計算されたRMSエラーと表面のRaは、2.0nmRMS粗さ要求に一致している。y(長さ)方向の表面のPSDからより詳細な表面像がわかる。示されている周波数は100μm〜0.5μmの周期に対応している。250mmに明らかなピークがあり、これはダイヤモンド工具の送り速度、4μm/1回転に対応している。
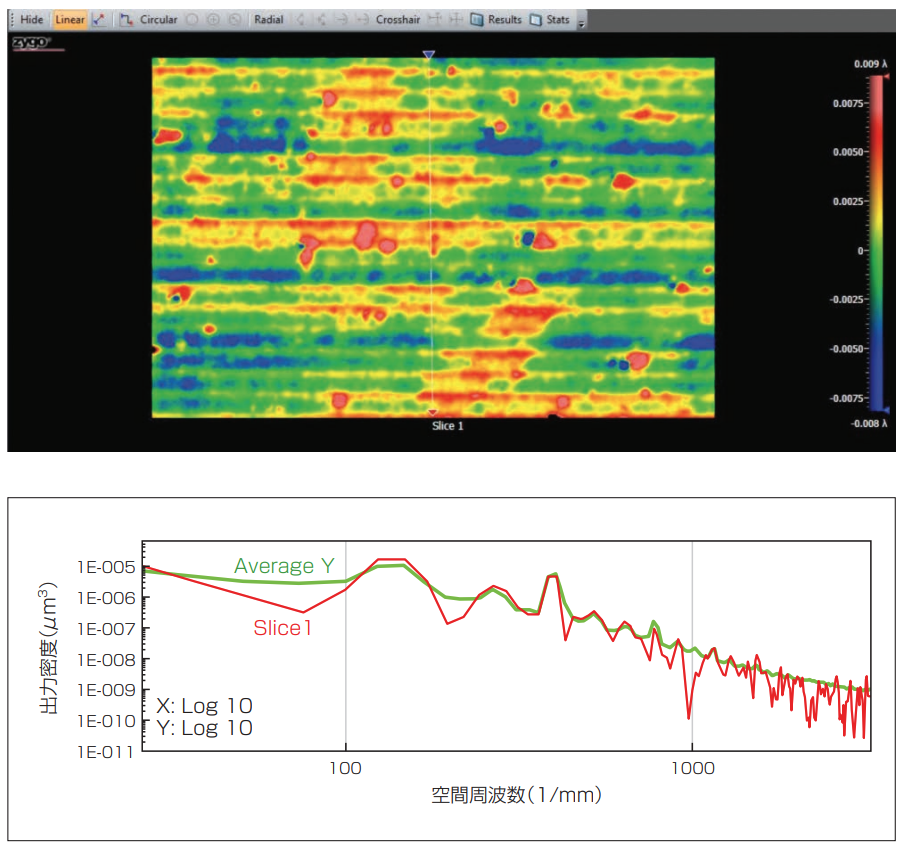
図1 ダイヤモンド研磨面NewView 3D光プロファイラからのパワースペクトル密度(PSD)は、100μm〜0.5μmの空間周期を含む(ZYGO社提供)。
パフォーマンスへのMSFの影響
表面エラーは光学パフォーマンスに影響を与える。影響は多様であり、システムの周波数成分、動作波長、設置場所に依存する。所与の周波数におけるエラーのパフォーマンスへの影響は、低、中、高空間周波数の境界を定めるひとつの方法である。低空間周波数エラー、パワー、非点収差、コマ収差、Z36 項までのゼルニケ多項式による説明、これらのエラーがシステムの点拡散関数(PSF)を広げる。高空間周波数エラーはシステムへの入射光、出射光のいずれについても光を高角度で拡散する。MSF エラーは、異なる領域に影響を与える。形状を変えずにPSFから出る光を拡散させるが、焦点面に射し込む程度に小さな角度では、像の暗い領域で陰の範囲がかすみ、わずかに減少する、あるいは画像の焦点からずれた部分の形状に起伏ができる。図2 は、MSF エラーがある場合とない場合のPSFへの影響を示している。
システムパフォーマンスに対するMSF エラーの詳細な分析はこの記事の範囲を超えるが、末尾の参考文献で見ることができる。いくつか役に立つように極めて単純化すると、影響の範囲と形がいくらか見えてくる。変調伝達関数(MTF)のようなパラメータは特に、MSF エラーが光を散乱させる角度に依存している。散乱角、ɵの推定は、回折格子の式、ɵ=arcsin(λ/d −sinɵi)で得られる。ここではɵiは入射角、d はグレーティングの周期(ここでは、表面エラーの周期)、λはシステムの動作波長。ここから、光はPSFのコアから回折することが分かる。その回折角は、システムの波長の関数、グレーティングの空間周波数(f =1/d )、あるいはエラー周期による。
ダイヤモンド回転工具のキズや軽量ミラーの構造の転写などの場合、この近似は非常によく当てはまる。よりランダムなエラーでは、散乱パタンは一定ではないが、最終的な光の位置に関しては、この回折格子の式はまだ有益な示唆を与えてくれる。例えば図1で、ダイヤモンド工具のキズは視野内約7°の角度で光を散乱させる。広帯域イメージングシステムでは、この表面は、修正されていない場合、明るいオブジェクトの周囲に不快な虹をかける、ピッチ研磨の表面ではこれはあり得ない。
MSFの高周波数限界は、散乱角度がシステムの口径に近づく点で規定されると考えてよい。この限界を越える状態は通常、表面粗さとして記述される。その点では、システムに対する影響は広範囲であり、システムを盲目にするようなぎらつきとなる。
回折限界PSFのピーク強度に関連するPSFコアの強度縮小は、ストレールレシオ(Strehl ratio)、または単にストレールと呼ばれる。小さなエラーの場合、ストレールの影響は次の式で近似できる。
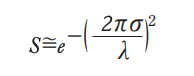
全積分散乱( TIS)の適切な近似は、TIS ≈(4πσ/λ)2。ここから直ちに、13.5nmで動作する極紫外(EUV)リソグラフィシステムが、193nmの液浸リソグラフィシステムで用いられる同等の表面と比較して、200 倍多くのエネルギーを散乱することが明らかになる。
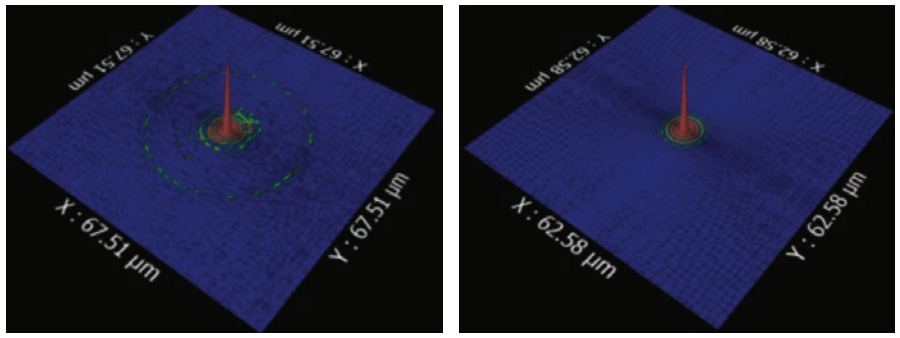
図2 点拡散関数(PSF)、MSFエラーをコントロールしていない場合と、した場合。
設計におけるMSF
最も要求の厳しいアプリケーションでは、光学設計者の目標−高品質で製造可能なアセンブリ方法を決定し、仕様化すること−は、全開口ピッチ研磨から高速で新しい機械研磨光学部品に移行するときに、MSFの結果が認められないことによって阻まれた。周波数に対する表面公差の設計と仕様化の範囲でMSF に注意することが現在重要となっている。
光学システムあるいは素子の設計中に、MSF エラーは通常、公差の中で考慮される。これは、波面設計が半径と言った低周波数の条件、一般的な非球面条件の小数の係数、あるいはゼルニケ多項式によってコントロールされているためである。この意味で、最初のゼルニケ(イメージング開口にわたり約5周期)に代表されるよりも高い空間周波数がMSF に対して無理のない、より低い限界となるかも知れない。
光学設計ソフトウエアは、システムにおける散乱、MSFへのその影響をモデリングする機能、その他のパラメータを含んでいる。例えば、Code V(米シノプシス社)やZemax(米レイディアント・ゼマックス社)は、いくつかの散乱関数を含んでおり、これらは表面に適用でき、次に不連続な光線追跡やイメージング解析ツールを使って評価できる。
(もっと読む場合は出典元へ)
出典元
https://ex-press.jp/wp-content/uploads/2014/02/0016feature01.pdf
