フーリエ積分

パルスの繰り返し空間周期 λ = 1 cm、パルス幅 λ/a、a = 4 の場合を考える（図１）。（注. λは光波長ではなく、単にパルス波形の周期を示す。下記のkも光の波数でなく、一般的な空間角周波数を示す。）波形f(x)は偶関数であるからフーリエ級数は余弦級数のみである。

余弦級数係数A_mの求め方はフーリエ級数で解説している。空間周波数と対応付ければ空間周波数スペクトルとなる（図１aグラフ）。
次に、パルス幅を変えずにパルス間隔を大きくする。λ = 2cm・4cm、a = 8・16としたときの波形 f(x) と空間周波数スペクトルを図１b・c に示す。図から明らかなように、空間周波数スペクトル全体形状は変化せず、各成分の周波数間隔が減少する。

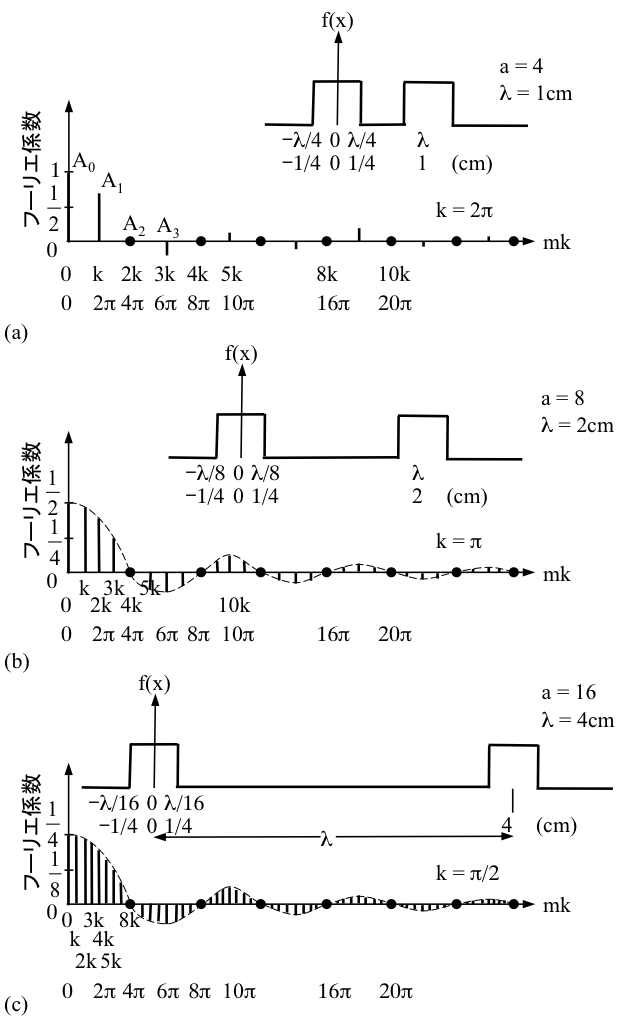
図 １　パルス間隔を広げた極限が(孤立)矩形パルスとなる。間隔が広がるにしたがって、より多くの周波数項が付け加わる。

λ無限大の極限では、空間周波数スペクトルは連続となる。mk をあらためてkとおくと、空間周波数スペクトルはk の連続関数となる。
空間周波数スペクトルが連続になるのに対応して、フーリエ級数はフーリエ積分で置き換えられて以下のようになる。