電流iが流れる直線状ワイヤと直交する面内で、ワイヤを中止とする半径rの仮想的円周を考える(図)。円周上の磁界Bは接線方向を向き、その大きさはB=μ0i / (2πr)であることが実験的に分かる。ワイヤを囲む仮想的円周をCとすると、
![]()
となる。Cを円周でなく、径方向微小線素と(半径の異なる)円周方向微小線素からなる折れ線としても上式は成立する。径方向線素の積分は、Bとdlが直交するためゼロであり、円周方向積分和はμ0iとなる。以上から、複数のワイヤがあり、それらを囲む任意の閉曲線をCとするとき、
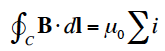
となることが分かる。これがアンペールの法則である。
断面内で電流が分布している場合、アンペールの法則は、
![]()
となる。ここで、Jは電流密度である。開曲面Aの縁が閉曲線Cである。μ0は自由空間の透磁率で、4π×10-7 Ns2C-2である。物質の透磁率μは、
![]()
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
