伝搬方程式である非線形シュレディンガー方程式は非線形偏微分方程式であり、一般的に解析的な解を求めることができない。従って、光ファイバーにおける非線形光学効果を理解するために数値解析が用いられている。ここでは数値計算方法として、スプリットステップフーリエ法を取り上げ、光ファイバー中のパルスの振る舞いの解析方法を説明する。スプリットステップフーリエ法は高速フーリエ変換のアルゴリズム(FFT)を用いているために、他の大部分の解析法に比べて相対的に高速な解析が可能となる。
スプリットステップフーリエ法の説明を行うにあたり、非線形シュレディンガー方程式を用いる。まず同式を形式的に次のように変形すると都合がよい。

ただし、Dˆは線形媒質の分散と吸収を表す微分演算子、Nˆは非線形演算子であり、パルス伝搬に対するファイバーの非線形性の影響を表すものである。これらの演算子は次式で与えられる。
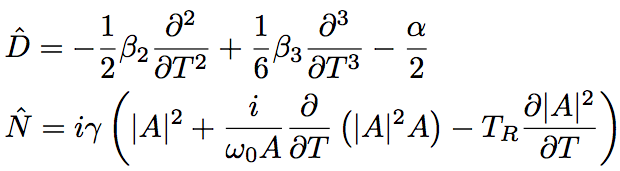
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。