光ファイバー中の光波の伝搬はマクスウェル方程式により記述することができる。通常は計算を簡略化するために電場の急変動成分を無視して緩変動包絡線の近似が用いられる。パルスの群速度で移動する時間系 (遅延座標系) を用いて、光パルスの包絡線関数 A(z, T) に対する伝搬方程式を表すと以下のようになる。
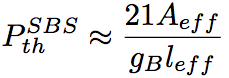
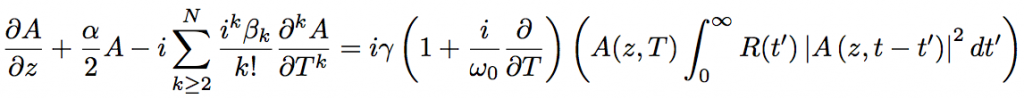
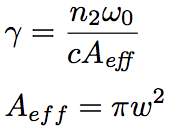
この式は非線形シュレディンガー方程式と呼ばれ、光ファイバー中における超短パルスの伝搬を記述するのによく用いられる。γ は非線形係数である。この式において左辺の第 2 項はファイバー損失を、第 3 項は高次分散を含めた波長分散の効果を表している。右辺は全体で自己位相変調や四光波混合、自己急峻化、誘導ラマン散乱などの非線形光学効果を含んでいる。ここで R(t) はラマン応答関数であり、電子遷移と振動遷移 (ラマン) の寄与の両方を含んでいる。図1はラマン利得スペクトルから求めた遅延ラマン応答関数 hR(t)(実験値) である。
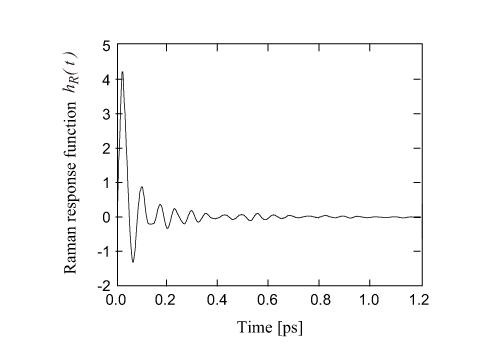
図1:ラマン利得応答関数
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。