分散とは、波長により光の伝搬時間に遅延が生じる現象を言う。光パルスが分散の影響を受けるとパルスは広がってしまう。光パルスが分散性媒質を通ることにより、分散効果を受ける様子を図1に示す。モード分散や偏波モード分散も光ファイバーの分散であるが、通常、分散と言えば波長分散を指す。
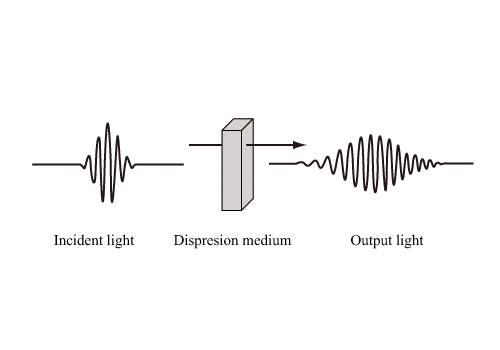
図1:分散の概念図
波長分散はさらに、材料の屈折率変化による材料分散と導波路構造による導波路分散に分けられる(波長分散は材料分散と導波路分散の和である)。ここで材料分散は石英ガラスなどの物質特有のものであり、変化させることは困難であるが、導波路分散はコアの半径や比屈折率差、屈折率分布などを調節することにより制御できる。
波長分散の原因は、誘導性媒質が屈折率の周波数依存性(波長依存性)を持つことによる。なぜなら、屈折率n(λ)の媒質中を伝搬する光の速度は、真空中の光の速度cを用いるとc/n(λ)で表され、異なる波長の光の速度に差が生まれるためである。
媒質の屈折率n(λ)は、1871年にW.Sellmeierが導出したセルマイヤーの分散式(The Sellmeier equation)を用いて次式のように表すことができる。
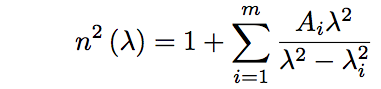 …(1)
…(1)
ここでAi、λi μmは物質により異なり、実験的に求められている定数である。Aiは共鳴振動数νiの強度であり、λiは真空中の光の速度cと共鳴振動数νiを用いてλi=c/νiで示される。
セルマイヤーの分散式は、共鳴振動数ν0において発散してしまうため、その近傍で正しい結果を得ることは困難であるが、それ以外の領域において良い近似を得ることができる(m=3、365~2325nmの範囲で屈折率の計算精度±5×10−6である[1])。様々な媒質の定数Ai、λiはE.D.Palikの“Handbook of Optical Constancts of Solids”[2]で確認することができる。常温18℃でのシリカガラスでは、m=3でA1=0.6961663、A2=0.4079426、A3=0.8974794、λ1=0.0684043、λ2=0.1162414、λ3=9.896161が知られており[3]、屈折率は波長の増加と共に減少する。
式(1)を屈折率の周波数依存性n(ω)に書き直すと
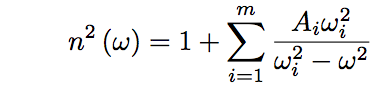
無料ユーザー登録
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。