光ファイバーの分散パラメータを示すために、モードの伝搬定数βを中心周波数ω0のまわりでテイラー展開すると次式で表される。
![]() …(1)
…(1)
ここで、
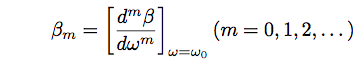
である。パラメータβ1、β2は屈折率nとその導関数
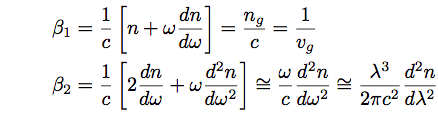
に関連づけられる。ここで、ngは群屈折率、vgは群速度である。β1=1/vgは単位長さあたりの伝搬遅延時間で群遅延時間と呼ばれる。また、β2はパルスの広がりを示す群速度分散(GVD)である。図1(a)にバルク型のシリカガラスの屈折率n、群屈折率ng、図1(b)に群速度分散β2の波長依存性を示す。図中のλDは分散がゼロとなるゼロ分散波長であり、シリカガラスの場合1.27μm付近にある。シリカガラスの屈折率から導かれるこの分散は材料分散と呼ばれる。実際の光ファイバーでは、コアに少量のGeO2やP2O5などのドーパントが入っており、濃度によって分散特性が変わる[1]。屈折率nが大きな物質は群速度分散β2の絶対値も大きい傾向にある。
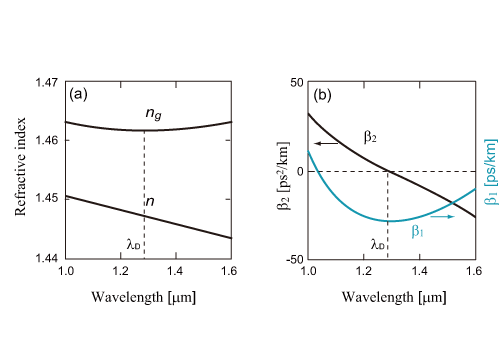
図1:シリカガラスの分散特性。
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。